从小学起,我们就已经开始接触了各种图形;到了初中,我们就开始学习这些图形的相关性质;之后的学习,无非就是衍生得更深入罢了。今天,小编在这里讲的是有关三角形的内容。三角形中线有什么性质?三角形中线定理是什么?接下来就让小编带大家一起来了解了解吧。
中线定义
三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线。任何三角形都有三条中线,而且这三条中线都在三角形的内部,并交于一点。
由定义可知,三角形的中线是一条线段。由于三角形有三条边,所以一个三角形有三条中线,且三条中线交于一点,这点称为三角形的重心。每条三角形中线分得的两个三角形面积相等。
中线性质
设⊿ABC的角A、B、C的对边分别为a、b、c。
1、三角形的三条中线都在三角形内。
2、三角形中线长:
ma=(1/2)√2b^2+2c^2-a^2;
mb=(1/2)√2c²+2a²-b² ;
mc=(1/2)√2a²+2b²-c² 。
(ma,mb,mc分别为角A,B,C所对的中线长)
3、三角形的三条中线交于一点,该点叫做三角形的重心。
4、直角三角形斜边上的中线等于斜边的一半。
5、三角形中线组成的三角形面积等于这个三角形面积的3/4。
中线定理
中线定理(Apollonius's theorem),又称阿波罗尼奥斯定理,是欧氏几何的定理,表述三角形三边和中线长度关系。
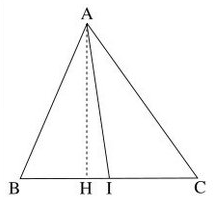
定理内容:三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。即,对任意三角形△ABC,设I是线段BC的中点,AI为中线,则有如下关系:
AB²+AC²=2(BI²+AI²)或作AB²+AC²=1/2(BC)²+2AI²
证明:勾股定理AB+AC=(AH+BH)+(AH+HC)
=2(AI-HI)+(BI-HI)+(CI+HI)
=2AI-2HI+BI+HI-2BIHI+CI+HI+2CLHI
=2AI+BI+CI
=2(BI+AI)
三角形主要有五条性质,中线定理就是根据这些性质所衍生出来的。在平时的解题过程中,我们要学会融会贯通,各种性质相结合,灵活地去运用。在中长线选股策略方面,也亦如此,这样才能选到一只好股。
相关阅读推荐:
对于三角形整理K线形态及买点的分析
怎么掌握K线上升三角形形态?
K线下降三角形形态是如何表现的?
